Calcul quantique de structure électronique

Notre étude porte sur les réactions chimiques conduisant à la formation d'agrégats de silicium, par conséquent, les potentiels-modèle de dynamique moléculaire précédemment cités ne sont pas suffisants pour traduire toute la complexité des phénomènes mis en jeu. En effet, le silicium passe souvent pas des états d'hybridation d'orbitales atomiques différents. Par conséquent le potentiel change en fonction des atomes voisins, et donc change pendant la simulation. Il devient donc nécessaire de passer par des méthodes quantiques pour trouver la distribution spatiale du potentiel d'interaction en fonction du temps pour déduire les positions des atomes dans un algorithme de calcul de trajectoire. Dans les méthodes de calculs de trajectoires que nous venons de décrire, nous avons des équations qui font intervenir des positions et des vitesses. Cependant un des postulats fondamentaux de la mécanique quantique consiste à supposer que les particules ne peuvent être décrites par un couple position-impulsion. En effet ces grandeurs ne sont pas mesurables simultanément avec une précision infinie du fait de la dualité onde-corpuscule. Par exemple l'expérience des fentes d'Young [32] réalisée sur des électrons montre que ceux-ci diffractent et développent une figure d'interférences. Pourtant comme Einstein l'a montré dans son article sur l'effet photoélectrique, les photons sont bien des particules dont l'énergie est quantifiée [33]. La seule explication possible pour accorder ces deux phénomènes est de considérer l'électron comme une particule qui ne peut être décrite que par une densité de probabilité de présence. On introduit donc une fonction qui va permettre de calculer cette probabilité de présence : la fonction d'onde $\psi$ . Cette fonction d'onde est, comme son nom l'indique, une onde qui a une fréquence qui varie linéairement avec l'énergie. Les niveaux atomiques en sont la preuve la plus directe. Les électrons gravitent autour du noyau des atomes et n'absorbent que des quantités discrètes d'énergie pour changer d'orbite [34]. Nous avons donc $E=h\nu=p^2/2m$ . Nous avons aussi le critère de Rayleigh qui nous dit que deux sources de longueurs d'onde définies ne peuvent être distinguées au dessous d'une certaine distance qui est fonction de la longueur d'onde. Ainsi, pour nos fonctions d'onde, il est impossible de mesurer simultanément la position et l'impulsion ( proportionnelle à la fréquence ) avec une précision supérieure à une quantité très petite de l'ordre de $\Delta p \Delta q \geq \hbar /2$ où $\hbar$ est la constante de Planck. Cette relation est appelée "inégalité de Heisenberg". Les tentatives pour raccorder la mécanique classique de Newton avec ces fonctions d'onde ont montré que celles-ci évoluent dans un espace hermitien dans lequel les actions sur les fonctions d'onde sont décrites en terme d'opérateurs. Il a aussi été montré que le formalisme de Hamilton, étant donné sa capacité à décrire les équations du mouvement uniquement à partir des positions et des impulsions était parfaitement adapté pour trouver les équations des trajectoires tout en tenant compte de l'impossibilité d'une description simultanée de la position et de la quantité de mouvement.

Nous utilisons donc l'hamiltonien

$$H=p^2/2m + V(\vec q)$$ (2.15)

où p est l'impulsion et q la position.

avec

$$\frac{d \vec q}{d t}=\frac{\partial H}{\partial \vec p}$$ (2.16)

et

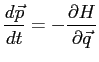$$\frac{d \vec p}{d t}= - \frac{\partial H}{\partial \vec q}$$ (2.17)

Ces équations donnent un système qui amène à une équation aux dérivées partielles, qui, une fois résolue, donne l'équation de trajectoire.

L'impossibilité de mesurer la position r et l'impulsion p simultanément impose de décrire la trajectoire avec une de ces deux variables et de déduire ce qu'il advient de l'autre par un changement de référentiel (base). La nature hermitienne de l'espace, d'un point de vue quantique, impose le passage de l'écriture des impulsions dans l'espace des positions comme proportionnelle à l'opérateur de gradient $\vec p = \hbar /i \vec \nabla$ avec $i$ le nombre imaginaire pur. Armés de ces outils mathématiques de l'espace quantique, nous pouvons nous attaquer à la description de la nature des réactions chimiques, et donc à leur modélisation.