Hamiltonien général

Nous pouvons trouver la fonction d'onde $\psi$ d'un système en résolvant l'équation aux valeurs propres $H \psi = E \psi$ , où H est l'hamiltonien du système [35,36,37]. L'hamiltonien représente l'énergie totale d'un système. Dans le cas d'un atome ou d'une molécule, celui-ci est composé de la somme des énergies cinétique et potentielle de l'ensemble des particules (noyaux et électrons) présentes. Dans le formalisme quantique, il nous faut travailler dans une certaine représentation, c'est-à-dire dans un certain couple de variables qui ne peuvent être mesurées simultanément. Cette représentation peut être le couple position-impulsion ou encore angle-action, où n'importe quel couple de variables représentant notre problème, et qui ne commute pas pour les cas non triviaux. Par exemple:

$$\vec p \vec q - \vec q \vec p \neq 0$$ (2.18)

Dans la représentation en position, l'impulsion est donnée par l'opérateur de gradient et la position est donnée par l'opérateur de multiplication par la coordonnée. Les différents termes qui composent l'hamiltonien sont donc uniquement des termes d'énergie cinétique et de potentiel électrique. L'énergie cinétique est donnée dans le système MKSA par:

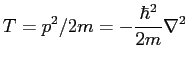$$T= p^2/2m= - \frac{\hbar^2}{2m} \nabla^2$$ (2.19)

et le potentiel électrique par

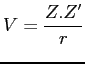$$V= \frac{Z.Z'}{r}$$ (2.20)

avec les charges $Z$ des particules séparées par la distance $r$ .

Ainsi pour une molécule nous obtenons

$$H_{tot} = V_{nn}+V_{ne}+V_{ee}+T_n +T_e$$

Où l'indice 'n' désigne les noyaux et l'indice 'e' les électrons.

$$H_{tot} = \sum_{A<B}\sum \frac{Z_A.Z_B}{r_{AB}} - \sum_A \sum_i \... ...{\hbar^2}{2 m_e} \sum_i \nabla^2_i - \frac{\hbar^2}{2 M_A} \sum_A \nabla^2_i$$

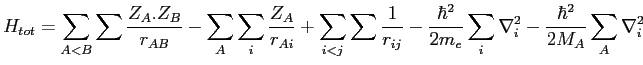
Où nous réservons les lettres majuscules pour les noyaux et les minuscules pour les électrons. r représente la distance, Z la charge du noyau considéré en unité de 'e' et $\hbar$ la constante de Planck. Cette équation représente un système d'équations différentielles composé d'un nombre d'équations égal au nombre de particules de la molécule. Résoudre cette équation est, sauf dans des cas très simples, très compliqué, et en général impossible sous forme analytique. En effet une simple molécule de $SiH_4$ comporte 18 électrons et 5 noyaux. La résolution numérique de toutes ces équations pour des agrégats est très longue malgré les moyens informatiques importants dont nous disposons actuellement. Il est donc nécessaire de recourir à des approximations si nous voulons pouvoir effectuer un calcul de structure électronique en fonction du temps, c'est-à-dire sur le grand nombre de positions qui constituent la totalité de la trajectoire.