L'approximation de Born-Oppenheimer

La première approximation que nous pouvons faire a été élaborée conjointement par Born et Oppenheimer en 1927 [38]. Elle consiste à prendre en compte l'énorme différence de masse qui existe entre les noyaux et les électrons. Nous remarquons que l'hamiltonien général peut être écrit comme la somme:

$$H_{tot} = V_{NN}+T_N +V_{Ne}+V_{ee}+T_e= H_N + H_{el}$$

avec

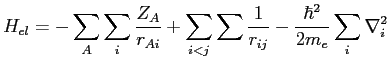$$H_{el} = - \sum_A \sum_i \frac {Z_A}{r_{Ai}} + \sum_{i<j} \sum \frac{1}{r_{ij}} - \frac{\hbar^2}{2 m_e} \sum_i \nabla^2_i$$ (2.21)

L'hamiltonien électronique $H_{el}$ dépend des coordonnées nucléaires, c'est pourquoi la partie de l'hamiltonien correspondant à l'énergie cinétique des noyaux ne commute pas avec l'hamiltonien électronique. Ainsi, nous ne pouvons pas, en toute rigueur, écrire la fonction d'onde totale $\psi_{tot}(\vec R_A,\vec r_i)$ comme étant le produit d'une fonction d'onde pour les noyaux par une fonction d'onde pour les électrons. Cependant les noyaux étant beaucoup plus lourds que les électrons, nous pouvons les considérer comme étant fixes lors du mouvement des électrons. Nous pouvons donc effectuer une séparation adiabatique et écrire ce que nous appelons l'approximation de Born-Oppenheimer, c'est-à-dire une séparation de la fonction d'onde entre une partie pour les noyaux (fonction de $R_A$ ) et une autre pour les électrons lorsque les noyaux sont dans une position $R_A$ (fonction de $r_i$ connaissant $R_A$ ):

$$\psi_{tot}(\vec R_A,\vec r_i )=\xi_n(R_A) \Phi(r_i \vert R_A)$$ (2.22)

Nous pouvons faire agir l'hamiltonien sur cette fonction d'onde:

$$H_{tot} \psi_{tot}(\vec R_A,\vec r_i ) = \xi_n(R_A) H_{el} \Phi(r_i \vert R_A) + [(V_{NN}+T_N)\xi_n(R_A)]\Phi(r_i \vert R_A)$$

$$+ [T_N \Phi(r_i \vert R_A)]\xi_n(R_A) - \frac{\hbar^2}{2 M_A} \sum_A \vec \nabla \Phi(r_i \vert R_A) \vec \nabla \xi_n(R_A)$$

En considérant que le terme $\Phi(r_i \vert R_A)$ ne dépend que faiblement des coordonnées des noyaux $R_A$ , nous pouvons considérer que les termes de couplage non-adiabatique

$$[T_N \Phi(r_i \vert R_A)]\xi_n(R_A)$$ (2.23)

et

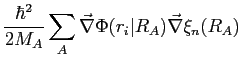$$\frac{\hbar^2}{2 M_A} \sum_A \vec \nabla \Phi(r_i \vert R_A) \vec \nabla \xi_n(R_A)$$ (2.24)

sont négligeables devant les autres. Ainsi l'hamiltonien électronique devient prépondérant et l'hamiltonien total se réduit à:

$$H_{tot} \xi_n(R_A) \Phi(r_i \vert R_A) = [T_N+V_{NN}+H_{el}]\xi_n(R_A) \Phi(r_i \vert R_A)$$ (2.25)

donc

$$H_{tot} \xi_n(R_A) = [T_N+V_{NN}+H_{el}]\xi_n(R_A)$$ (2.26)

représente une équation aux valeurs propres agissant sur la fonction d'onde nucléaire qui détermine les états rotationnels et vibrationnels des noyaux. Nous obtenons ainsi un potentiel effectif $V_{NN}+H_{el}$ agissant sur les noyaux. Nous l'appelons surface de potentiel. Ainsi l'approximation de Born-Oppenheimer nous permet de découpler la fonction d'onde en une partie électronique et une partie nucléaire, ce qui va permettre de ne calculer que la partie électronique pour en déduire les forces inter-nucléaire et donc le mouvement des noyaux dans un algorithme (Gear ou Verlet) précédemment cité.