Le déterminant de Slater

La fonction d'onde électronique doit être considérée comme contenant des électrons qui sont indiscernables les uns des autres. Nous pouvons déduire de cela que l'échange d'un électron avec un autre de même spin ne doit pas changer la valeur de la densité de probabilité associée à la fonction d'onde ( $\langle\psi\vert\psi\rangle$ ). Ceci a des conséquences, compte tenu des configurations où nous échangeons les électrons qui doivent, par définition, être identiques. Une approximation sur notre fonction d'onde électronique $\Phi(r_i \vert R_A)$ des 2n électrons, consiste à l'écrire comme un produit de fonctions d'onde mono-électronique:

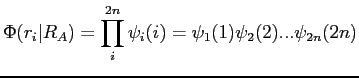$$\Phi(r_i \vert R_A) = \prod_{i}^{2n} \psi_i (i) = \psi_1(1)\psi_2(2)...\psi_{2n}(2n)$$ (2.27)

où l'indice i représente l'orbitale i. Pour rendre constante la norme de notre fonction d'onde lors de l'échange de deux particules, il faut que l'opération d'échange de deux particules transforme la fonction d'onde en elle même (particules symétriques ou bosons) pour les particules de spin entier

$$\psi_1^*(1)\psi_2(2)=\psi_1^*(2)\psi_2(1)$$ (2.28)

ou en son inverse (particules antisymétriques ou fermions) pour les particules de spin demi-entier

$$\psi_1^*(1)\psi_2(2)=-\psi_1^*(2)\psi_2(1)$$ (2.29)

ce qui est le cas des électrons qui sont des fermions. En effet dans les deux cas ci-dessus, la densité de probabilité de présence reste la même $\int_{\Re} \psi_1^*(1)\psi_2^*(2).\psi_1(1)\psi_2(2) d^3r = \int_{\Re} (-\psi_1^*(2)\psi_2^*(1))(-\psi_1(2)\psi_2(1)) d^3r$ quand on intègre sur tout l'espace $\Re$ en utilisant les variables d'intégrations $d^3r=dx.dy.dz$ .

Les électrons étant des fermions, nous devons avoir la fonction d'onde qui contient toutes les permutations possibles ce qui permet d'écrire la fonction d'onde comme le déterminant:

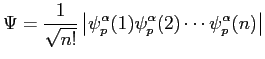$$\Psi = \frac{1} {\sqrt{n!}} \left\vert \psi_p^{\alpha}(1) \psi_p^{\alpha}(2) \cdots \psi_p^{\alpha}(n)\right\vert$$ (2.30)

avec $\psi_p^{\alpha}(1)$ la fonction d'onde du premier électron de spin $\alpha$ dans l'état p. Le coefficient $n!^{1/2}$ provient de la normalisation de cette fonction d'onde. L'écriture sous cette forme de la fonction d'onde permet de déduire le principe de Pauli [39]. En effet deux électrons ne peuvent se trouver dans le même état, c'est-à-dire qu'ils ne peuvent pas avoir la même fonction d'onde. L'écriture de la fonction d'onde sous la forme d'un déterminant de Slater nous donne une fonction d'onde nulle dans le cas où deux colonnes du déterminant sont identiques, c'est-à-dire si deux électrons sont dans le même état et partagent la même fonction d'onde.