Combinaison linéaire d'orbitales atomiques

La dernière approximation que nous allons utiliser était proposée par Mulliken [40] et consiste à écrire la partie électronique de notre fonction d'onde comme étant une combinaison linéaire d'orbitales atomiques (Linear Combination of Atomic Orbitals , méthode LCAO). Les fonctions d'onde peuvent donc être décomposées sur une base d'orbitales. Les fonctions propres de cette base peuvent être issues du calcul des différentes orbitales de l'atome d'hydrogène obtenues en résolvant analytiquement l'équation de Schrödinger pour un électron dans un potentiel central:

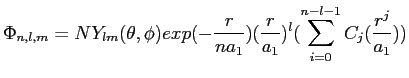$\displaystyle \Phi_{n,l,m}=NY_{lm}(\theta,\phi)exp(-\frac{r}{na_1}) (\frac{r}{a_1})^l (\sum_{i=0}^{n-l-1}C_j(\frac{r^j}{a_1}))$

(2.31)

où $a_1=\hbar^2/(m_e e^2)\sim 0.053$ nm, les sont les coefficients des polynômes de Laguerre [41], $Y_{lm}(\theta,\phi)$ les harmoniques sphériques qui sont les fonctions propres des opérateurs décrivant le moment cinétique orbital:

$\displaystyle L^2Y_{l,m}(\theta,\phi)=l(l+1)\hbar^2Y_{l,m}(\theta,\phi) L_zY_{l,m}(\theta,\phi)=m\hbar Y_{l,m}(\theta,\phi)$

(2.32)

c'est-à-dire, pour l=0 :

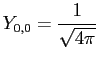$\displaystyle Y_{0,0}=\frac{1}{\sqrt{4\pi}}$

(2.33)

et pour l=1 :

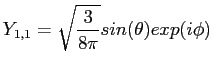$\displaystyle Y_{1,1}=\sqrt{\frac{3}{8\pi}}sin(\theta) exp(i\phi)$

(2.34)

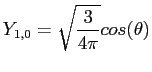$\displaystyle Y_{1,0}=\sqrt{\frac{3}{4\pi}}cos(\theta)$

(2.35)

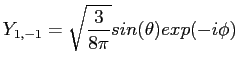$\displaystyle Y_{1,-1}=\sqrt{\frac{3}{8\pi}}sin(\theta)exp(-i\phi)$

(2.36)

Ainsi, la donnée d'une fonction d'onde revient à trouver les coefficients $\alpha_k$ de décomposition de celle-ci sur la base constituée par les orbitales atomiques $\Phi_k(r)=\Phi_{n,l,m}(r)$ d'atomes hydrogénoïdes.

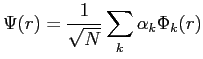$\displaystyle \Psi(r)=\frac{1}{\sqrt{N}}\sum_k \alpha_k \Phi_k(r)$

(2.37)

avec

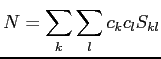$\displaystyle N=\sum_k\sum_l c_k c_l S_{kl}$

(2.38)

où $S_{kl}$ est le recouvrement entre les orbitales atomiques $\int \Phi_k \Phi_l d^3 r$ [42].

Pour trouver ces coefficients $\alpha_k$ , plusieurs méthodes sont possibles. Cependant pour des raisons de temps de calcul la méthode que nous employons consiste à passer par une minimisation des coefficients par rapport à l'énergie. En effet les électrons se placent dans la configuration de plus basse énergie étant donné leur grande mobilité par rapport aux noyaux. Ce minimum est trouvé par la méthode de Hartree-Fock non restreinte. Cette méthode est dite non restreinte car elle garde la fonction d'onde sous une forme spin-orbitale, c'est-à-dire sous la forme d'un produit entre une partie spatiale et une partie de spin. En effet, deux électrons de spin différents vont ressentir des potentiels de valeur voisine, mais néanmoins différents.