L'équation de Hartree-Fock Roothaan

Nous pouvons décomposer l'hamiltonien électronique comme la somme de deux termes. L'un pour décrire l'effet que ressentent les électrons sous l'influence des noyaux (élaboré par Hartree) et l'autre terme pour l'effet que ressentent les électrons sous l'influence des autres électrons (élaboré par Fock):

$$H = H_1+H_2$$ (2.39)

$$H_1 = - \sum_A \sum_i \frac {Z_A}{r_{Ai}} - \frac{\hbar^2}{2 \pi m_e} \sum_i \nabla^2_i$$ (2.40)

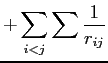$$H_2 = + \sum_{i<j} \sum \frac{1}{r_{ij}}$$ (2.41)

Dans la suite nous poserons $d\tau=dx.dy.dz.dp_x.dp_y.dp_z$ et nous omettrons les bornes sur les intégrales qui porterons toujours sur tout l'espace. Nous obtenons ainsi

$$E_{el}=\int\Psi^* H_1 \Psi d\tau + \int\Psi^* H_2\Psi d\tau= E_1 + E_2$$ (2.42)

qui devient, en remplaçant $\Psi$ par son expression sous la forme d'un déterminant de Slater, et compte tenu de l'orthogonalité et du fait que les fonctions d'onde sont normées :

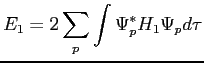$$E_1=2\sum_p \int \Psi_p^* H_1 \Psi_p d\tau$$ (2.43)

et

$$E_2=2\sum_p\sum_q[\int\Psi^*_p(i)\Psi^*_q(j)H_2\Psi_p(i)\Psi_q(j)... ..._j -\frac{1}{2}\int\Psi^*_p(i)\Psi^*_q(j)H_2\Psi_p(j)\Psi_q(i) d\tau_i d\tau_j]$$ (2.44)

où les fonctions $\Psi_p$ et $\Psi_q$ ne contiennent pas le spin et peuvent donc être égales à $\Psi_p^{\alpha}$ ou $\Psi_p^{\beta}$ et $\Psi_q^{\alpha}$ ou $\Psi_q^{\beta}$ respectivement.

L'énergie électronique totale devient donc la somme de ces deux énergies. En introduisant la décomposition des fonctions d'onde électroniques sur une base de fonctions d'onde atomiques (LCAO) :

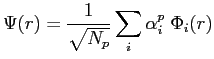$$\Psi(r)=\frac{1}{\sqrt{N_p}}\sum_i \alpha_i^p \;\Phi_i(r)$$ (2.45)

avec cette fois ci

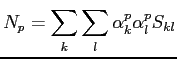$$N_p=\sum_k\sum_l \alpha_k^p\alpha_l^p S_{kl}$$ (2.46)

nous obtenons

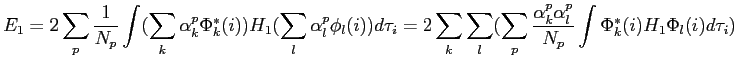$$E_1=2\sum_p \frac{1}{N_p} \int (\sum_k \alpha_k^p \Phi^*_k(i))H_1... ...\sum_p \frac {\alpha_k^p\alpha_l^p}{N_p} \int\Phi^*_k(i) H_1 \Phi_l(i) d\tau_i)$$ (2.47)

Nous noterons par la suite $P_{kl}=2\sum_{p} (\alpha_k\alpha_l/N_p)$ et donc nous pouvons réécrire $E_1$ comme :

$$E_1=\sum_k\sum_lP_{kl}H_{kl}$$ (2.48)

De la même façon :

$$E_2 = \frac{1}{2} \sum_k\sum_l\sum_m\sum_n P_{kl} P_{mn}[\int\Phi^*_k(i)\Phi^*_m(j)H_2\Phi_l(i)\Phi_n(j) d\tau_id\tau_j$$ (2.49)

$$- \frac{1}{2} \int \Phi^*_k(i)\Phi^*_m(j) H_2 \Phi_l(j) \Phi_n(i) d\tau_i d\tau_j]$$

que nous renoterons aussi

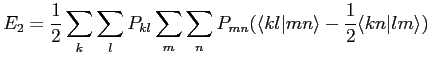$$E_2=\frac{1}{2} \sum_k \sum_l P_{kl}\sum_m \sum_n P_{mn} ( \langle kl\vert mn \rangle -\frac{1}{2}\langle kn\vert lm \rangle )$$ (2.50)

Cette équation est la partie maîtresse de notre modélisation. Elle est connue sous le nom d'équation de Fock-Roothaan Hall [43,44] et va nous servir à déterminer la décomposition de nos fonctions d'onde électroniques sur notre base d'orbitales atomiques et donc la densité de probabilité de présence des électrons autour des atomes. L'utilisation d'une base de fonctions d'onde de type Slater, c'est à dire de fonctions d'onde obtenues par calcul analytique des orbitales de l'atome d'hydrogène, est une très bonne approximation dans le cas où les mouvements des électrons ne sont pas corrélés avec les mouvements des noyaux.