Méthodes paramétriques

La diagonalisation du déterminant séculaire reste encore un calcul lourd lorsque le nombre de fonctions d'onde mis en jeu est important. Ainsi, le but étant de réaliser une simulation de la dynamique moléculaire, le déterminant devra être calculé un très grand nombre de fois et doit donc être encore simplifié. Pour ce faire nous pouvons remplacer par des valeurs empiriques, un certain nombre de termes dans le calcul des intégrales d'échange et en déduire l'effet que va ressentir un électron, par la modification de son potentiel électronique sous l'influence de l'atome voisin, et de l'influence que peut avoir un autre atome voisin sur le deuxième voisin. De cette façon, seuls les termes de premier ordre seront considérés à ce niveau d'approximation. Les interactions entre les atomes se feront uniquement par l'interaction des premiers voisins. Nous écrirons donc pour les électrons :

$$E_{el}=f(P_{ii},U_{ii},\langle ii\vert jj \rangle , \langle ij\vert ji \rangle )$$ (2.56)

avec, $U_{ii}$ l'énergie d'un électron de valence sous la forme d'un atome hydrogénoïde c'est-à-dire l'énergie d'un électron dans sa couche sans l'effet d'écrantage que subissent les électrons de coeur. $P_{ii}$ est l'état fondamental de l'atome constitué de ces électrons de coeur et les interactions entre les électrons de valence. Pour une base de type Slater constituée d'orbitales atomiques s et p, les interactions des électrons de valence sont:

$$\langle ss\vert ss \rangle = G_{ss}$$

$$\langle ss\vert pp \rangle = G_{sp}$$

$$\langle pp\vert pp \rangle = G_{pp}$$

$$\langle pp\vert p'p' \rangle = G_{p2}$$

$$\langle sp\vert sp \rangle = H_{sp}$$

où $p'$ est une orbitale p d'un autre atome que l'atome considéré.

Les noyaux ont quant à eux une énergie de répulsion:

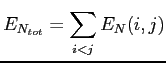$$E_{N_{tot}}=\sum_{i<j}E_N(i,j)$$ (2.57)

avec:

$$E_N(i,j) = Z_A.Z_B \langle AA\vert BB \rangle (1+e^{(-\alpha_A R_{ij})}+ e^{(-\alpha_B R_{ij})})$$

$$+ \frac{Z_iZ_j}{R_{ij}}(\sum_k a_{k_A} e^{-b_{k_A}(R_{ij}-c_{k_A})^2} +\sum_k a_{k_B} e^{-b_{k_B}(R_{ij}-c_{k_B})^2})$$

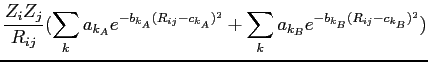où les coefficients $\alpha_i$ ,$a_{ki}$ ,$b_{ki}$ et $c_{ki}$ avec $i=A,B...$ sont des coefficients ajustés à partir des données spectroscopiques.

L'énergie électronique est quant à elle donnée par :

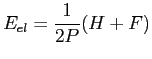$$E_{el}=\frac{1}{2P}(H+F)$$ (2.58)

avec P la densité électronique, H l'hamiltonien mono-électronique et F la matrice de Fock. Dans la matrice de Fock nous ne considérons que les termes mono et bi-électroniques. En ne considérant que les potentiels de premiers voisins nous avons les termes non diagonaux de la matrice de Fock:

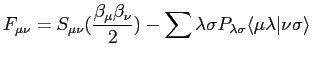$$F_{\mu\nu}=S_{\mu\nu}(\frac{\beta_{\mu}\beta_{\nu}}{2})-\sum{\lambda\sigma} P_{\lambda\sigma}\langle \mu\lambda\vert\nu\sigma \rangle$$ (2.59)

où $S_{\mu \nu}$ est le recouvrement d'orbitales, qui dans notre cas est un recouvrement d'orbitales de type Slater décrit au chapitre précédent. $\beta_{\mu}$ et $\beta_{\nu}$ sont quant à eux des paramètres ajustables avec des valeurs différentes selon le type d'orbitale (s ou p pour nous). Ainsi, le paramétrage pour l'hydrogène et le silicium sont connus [46] et nous avons :

	H	Si
$U_{ss}$	-13.073321	-26.763483
$U_{pp}$		-22.813635
$Z_s$	0.967807	1.635075
$Z_p$		1.313088
$\beta_s$	-5.626512	-2.862145
$\beta_p$		-3.933148
$G_{ss}$	14.794208	5.047196
$G_{sp}$		5.949057
$G_{pp}$		6.759367
$G_{p2}$		5.161297
$H_{sp}$		0.919832
$a_1$	1.128750	-0.390600
$b_1$	5.096282	6.000054
$a_2$	-1.060329	0.057259
$b_2$	6.003780	6.007183
$c_2$	1.570189	2.019987

L'utilisation de ces coefficients permet de ne pas calculer les termes de l'hamiltonien, mais simplement de les remplacer par leurs expressions empiriques. Ceci rend possible la minimisation de l'énergie électronique presque instantanément et rend donc accessible les lourds calculs de dynamique moléculaire. Les minimisations d'énergie à partir des méthodes de Hartree-Fock sont bien connues et nous pouvons aisément trouver des codes de calculs qui nous permettent de ne pas recoder toutes les primitives à utiliser. Cependant, une bonne compréhension des mécanismes physiques mis en jeu est nécessaire pour ne pas considérer une approximation qui ne serait pas valide, et qui nous conduirait à des résultats faux.