La méthode du champ auto-cohérent

Nous avons maintenant trouvé une façon de calculer rapidement l'hamiltonien, cependant nous ne savons toujours pas quelle est la fonction d'onde qui correspond au minimum d'énergie. Pour la trouver, nous utilisons une méthode itérative dite "méthode du champ auto-cohérent". Celle-ci consiste à se donner empiriquement une certaine projection de la fonction d'onde atomique sur la base LCAO décrite précédemment. Cette fonction d'onde permet une évaluation des éléments de la matrice de Fock $F_{kl}$ et donc permet de déterminer un ensemble initial de valeurs de $P_{mn}$ pour calculer le déterminant séculaire $\vert F_{kl}-E^pS_{kl}\vert$ . Ainsi, on trouve une valeur de l'énergie $E^p$ de l'orbitale moléculaire $\Psi^p$ et donc une nouvelle décomposition de la fonction d'onde donnée par un ensemble de coefficients $c_p$ . Ces nouveaux coefficients permettent de se donner une ré-évaluation des éléments de la matrice de Fock et de répéter la procédure jusqu'à atteindre une variation sur l'énergie suffisamment faible. Une fois que cette variation est faible, nous pouvons admettre que les coefficients de décomposition représentent bien la projection de la fonction d'onde correspondante à un minimum d'énergie. Pour nos simulations nous avons pris un critère d'arrêt de $10^{-7} kcal/mol$ . De cette façon, nous arrêtons la minimisation de l'énergie lorsque la variation sur l'énergie, sur une itération, est inférieure à notre critère d'arrêt. 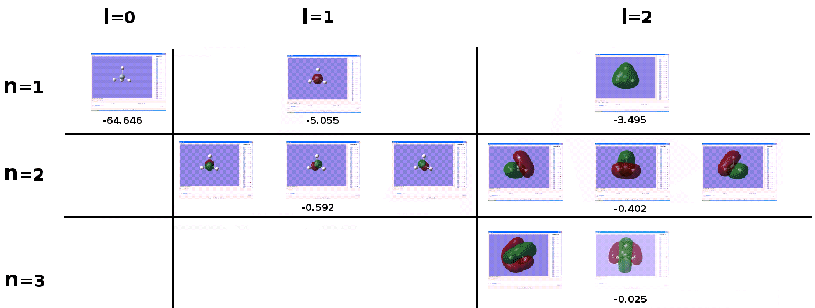Nous pouvons ainsi voir la distribution spatiale des fonctions d'onde associées à chaque niveau énergétique. Nous remarquerons en visualisant les différentes fonctions d'onde électroniques, que celles des molécules peuvent être des fonctions compliquées de l'espace (Fig 2.5). En connaissant la répartition spatiale des électrons nous pouvons déduire la force qu'ils vont engendrer sur les noyaux et nous pouvons utiliser les algorithmes classiques de trajectoires que nous avons décrit au début de ce chapitre.

Figure 2.5: Exemple de calcul d'orbitale moléculaire dans le cas d'une molécule de silane. Les orbitales sont représentées selon leur nombre quantique principale 'n' et leur nombre quantique angulaire 'l'. Nous donnons aussi la valeur énergétique de l'orbitale en unité atomique.