suivant: Méthodes paramétriques monter: L'équation de Hartree-Fock Roothaan précédent: L'équation de Hartree-Fock Roothaan Table des matières
Pour trouver la fonction d'onde électronique, ou plutôt sa décomposition sur la base de fonctions d'onde atomiques, nous supposons que le nuage électronique se place dans un état de minimum d'énergie. Ainsi, nous devons avoir un minimum d'énergie pour les coefficients qui vérifient:
 |
(2.51) |
quelque soit le coefficient de projection ![]() pour la fonction d'onde de l'électron p.
pour la fonction d'onde de l'électron p.
Ceci permet, en posant la matrice de Fock:
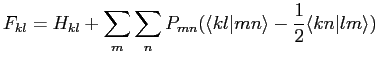 |
(2.52) |
de réécrire
![]() avec l'équation 2.44 comme:
avec l'équation 2.44 comme:
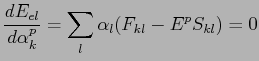 |
(2.53) |
où ![]() est l'énergie de l'orbitale
est l'énergie de l'orbitale
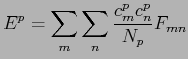 |
(2.54) |
Nous remarquons que la dérivée de l'énergie électronique doit être nulle pour tout
coefficient
![]() , ainsi nous devons avoir pour le déterminant :
, ainsi nous devons avoir pour le déterminant :
| (2.55) |
Ce déterminant, dit séculaire, permet de trouver la distribution des coefficients de projection des orbitales atomiques sur une base, compte tenu des relations d'orthogonalité et de normalisation des fonctions d'onde. En effet, nous pouvons évaluer le déterminant séculaire et obtenir sa valeur pour certains coefficients et voir comment il varie en fonction de ceux-ci. [45]