suivant: Calcul quantique de structure monter: Simulation de trajectoires précédent: L'algorithme de Verlet Table des matières
L'erreur commise par l'algorithme de Verlet est en
![]() .
Celle-ci peut être diminuée en augmentant
par exemple l'ordre du développement limité utilisé [29,30,31].
.
Celle-ci peut être diminuée en augmentant
par exemple l'ordre du développement limité utilisé [29,30,31].
Si nous prenons un développement de cinquième ordre, comme ce sera le cas dans nos simulations nous obtenons le système d'équations suivant:
![]()
![]()
![]()
![]()
![]()
![]()
La précision du développement en série de Taylor dépend de l'ordre de celui-ci. Nous appellerons les valeurs obtenues à partir du développement "valeurs prédites". Nous pouvons corriger ces valeurs en remarquant que la force, c'est-à-dire le gradient du potentiel est fonction de la position. Nous calculons à nouveau la valeur du potentiel, au niveau de la position prédite. Ainsi, nous déduisons une nouvelle valeur de l'accélération et donc une position différente pour le pas de temps suivant et ainsi l'erreur commise:
| (2.13) |
L'erreur sur l'accélération est ensuite utilisée pour corriger la position prédite. Dans cette équation nous réservons l'indice "pred" pour la valeur prédite et l'indice "corr" pour la valeur corrigée.
| (2.14) |
Ainsi, pour chaque composante du développement nous pouvons déduire une correction à ajouter à la prédiction. Cette correction est donnée par un ensemble de coefficients trouvés empiriquement pour avoir la meilleure stabilité de l'algorithme. Dans notre cas nous avons [29,30]:
L'algorithme de prédicteur-correcteur de Gear consiste donc à évaluer la
position au pas de temps suivant, de la même façon qu'avec l'algorithme de Verlet,
et de corriger l'erreur commise (
![]() )
par des pondérations visant à optimiser la
stabilité énergétique. Nous pouvons voir que cet algorithme est beaucoup plus précis
que l'algorithme de Verlet (Fig 2.4).
)
par des pondérations visant à optimiser la
stabilité énergétique. Nous pouvons voir que cet algorithme est beaucoup plus précis
que l'algorithme de Verlet (Fig 2.4).
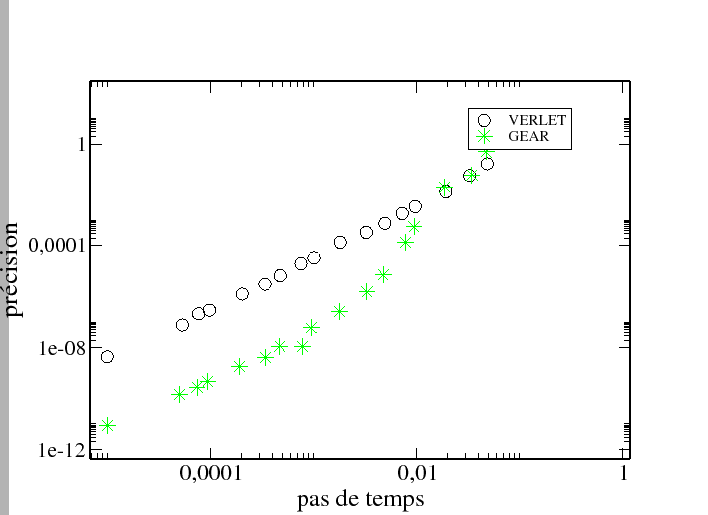
|