L'algorithme de Verlet

L'algorithme de Verlet est le premier à avoir été créé dans le calcul de trajectoire sur le principe d'un développement limité pas à pas. Verlet l'a utilisé avec succès avec les moyens informatiques limités de son époque pour déduire les propriétés thermodynamiques d'un gaz d'argon en supposant un potentiel d'interaction de Lennard-Jones entre les atomes qui s'écrit comme $V(\vec r_{ij})=4 \epsilon [ (\sigma / \vec r_{ij})^{12} - ( \sigma/ \vec r_{ij})^6 ]$ . Afin de faciliter les développements qui suivent nous utilisons fréquemment les unités réduites. Par exemple pour l'argon nous pouvons exprimer toutes les distances en unité de $\sigma = 0,3405 nm$ et toutes les énergies en unité d' $\epsilon = 119,8 ° K$ , où $\sigma$ est la distance d'équilibre entre deux atomes d'argon et $\epsilon$ la profondeur du puit de l'énergie de liaison. Nous obtenons de cette façon une unité de temps telle que la masse soit $m=48 \epsilon \sigma ^{-2}$ , c'est-à-dire que l'unité de temps devient $3.10^{-13}$ sec pour l'argon.  [27].

Pour obtenir les équations de trajectoire, nous écrivons la position à un instant $t+\Delta t$ comme un développement limité de deuxième ordre:

$$\vec r_i(t+\Delta t) = \vec r_i(t)+ \frac {\partial \vec r_i(t)}{... ...al t}\Delta t+\frac{1}{m_i}\sum_{i\neq j}{\vec F_{ij}}\Delta t^2+O(\Delta t ^3)$$ (2.7)

avec un potentiel tel que $\vec{F_{ij}}=\frac{-\partial}{\partial \vec r_{ij}} [V(\vec r_{ij})]$ . De la même façon nous avons :

$$\vec r_i(t-\Delta t) = \vec r_i(t)- \frac {\partial \vec r_i(t)}{... ...l t}\Delta t +\frac{1}{m_i}\sum_{i\neq j} \vec{F_{ij}}\Delta t^2-O(\Delta t ^3)$$ (2.8)

En combinant les équations ( 2.7) et (2.8) ci-dessus nous obtenons:

$$\vec r_i(t+\Delta t) = 2\vec r_i(t)- \vec r_i(t-\Delta t) +\frac{2}{m_i}\sum_{i\neq j} \vec{F_{ij}}\Delta t^2+O(\Delta t ^4)$$ (2.9)

et

$$\vec v_i(t)=\frac{\partial \vec r_i(t)}{ \partial t}= \frac { \vec r_i(t+\Delta t)-\vec r_i(t-\Delta t)} {2\Delta t} +O(\Delta t^3)$$ (2.10)

Nous pouvons donc obtenir la position à un temps $t+\Delta t$ connaissant la position à un temps $t$ et à un temps $t-\Delta t$ .

Avec cette méthode, Loup Verlet a trouvé avec succès les constantes thermodynamiques en étudiant un système de 864 particules.  [28]

De ce fait il a pu trouver les relations entre la température

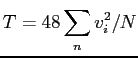$$T=48 \sum_{n} v_i^2 /N$$ (2.11)

dans les unités réduites avec N le nombre de particules. La pression peut être obtenue par le théorème du viriel:

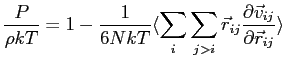$$\frac{P}{\rho k T} = 1 - \frac{1}{6NkT} \langle \sum_{i} \sum_{j>i} \vec r_{ij} \frac{ \partial \vec v_{ij}}{ \partial \vec r_{ij}} \rangle$$ (2.12)

Ainsi, il devient possible de remonter en simulation à des données comme la température de fusion en mesurant la mobilité des atomes en fonction de la température. Nous pouvons ainsi déduire toute grandeur macroscopique pour peu que nous connaissions son expression au niveau moléculaire en utilisant les conditions aux limites périodiques.