Première approche des méthodes de calcul des trajectoires

La méthode la plus simple pour calculer une trajectoire est la méthode d'Euler. Elle fut créée bien avant l'arrivée des premiers ordinateurs. Elle consiste à se baser sur le premier ordre du développement limité cité précédemment

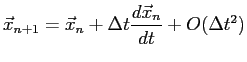$$\vec x_{n+1}=\vec x_n+ \Delta t \frac{d\vec x_n}{dt} + O(\Delta t ^2)$$ (2.3)

où $\Delta t$ est le pas de temps.
Géométriquement, cette méthode consiste à remplacer la courbe par une série de rectangles telle que la différence entre les hauteurs de deux rectangles consécutifs soit proportionnelle au produit de la dérivée par le pas de temps à l'instant considéré (Fig 2.2).

Figure 2.2: Visualisation graphique de l'approximation effectuée dans l'algorithme d'Euler.

Figure 2.3: Visualisation graphique de l'approximation effectuée dans l'algorithme de Runge-Kutta.

Une méthode un peu plus précise, la méthode de Runge-Kutta d'ordre deux, consiste à utiliser des triangles plutôt que des rectangles pour approximer la courbe en effectuant deux évaluations de la dérivée pour chaque pas de temps (Fig 2.3). L'une au début du pas de temps et l'autre à la fin:

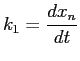$$k_1=\frac{dx_n}{dt}$$ (2.4)

et

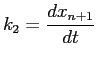$$k_2=\frac{dx_{n+1}}{dt}$$ (2.5)

Nous obtenons la valeur approximée de la courbe au pas de temps suivant par:

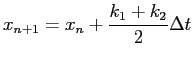$$x_{n+1}=x_n+ \frac{k_1+k_2}{2} \Delta t$$ (2.6)

La méthode de Runge-Kutta peut être généralisée à des ordres supérieurs, en effectuant un plus grand nombre d'évaluations de la fonction $x$ , ce qui permet de diminuer encore l'erreur commise. Cependant ces méthodes peuvent être améliorées dans le sens où le nombre de calculs à faire pour une précision voulue est encore important. Ainsi, d'autres méthodes plus performantes ont vu le jour. Ces méthodes permettent de suivre efficacement un grand nombre de trajectoires simultanément.