suivant: Première approche des méthodes monter: Simulation de la dynamique précédent: Simulation de la dynamique Table des matières
Dans ce chapitre nous allons voir une méthode pour résoudre les équations de trajectoires avec une méthode itérative qui peut être mise en oeuvre en simulation. La résolution des équations de trajectoires passe, depuis Newton par la résolution d'équations aux dérivées partielles [26].
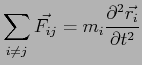 |
(2.1) |
Cependant la résolution systématique d'équations différentielles est un problème que personne
n'a pu résoudre, pas même les plus éminents mathématiciens.
C'est le cas lorsque les problèmes traitent de plus de trois corps.
Nous ne pouvons pas connaître la trajectoire précise, mais seulement
l'attracteur de la dynamique, c'est-à-dire les probabilités de trajectoires.
C'est pourquoi nous n'allons pas résoudre l'équation de la trajectoire analytiquement, mais
nous devrons recourir à des moyens alternatifs pour parvenir à nos fins.
Une de ces méthodes a été la méthode de Hamilton qui permet une mise en équation plus facile
en faisant appel à des coordonnées généralisées qui sont les coordonnées propres au problème.
Cependant ces méthodes restent basées sur la résolution d'équations aux dérivées partielles et
sont donc impossibles à résoudre dans la plupart des cas.
Pour résoudre ces équations aux dérivées partielles nous devons faire
des approximations, comme la résolution
des équations sur un maillage en temps discret à l'aide d'un développement en série de Taylor.
Nous pouvons donc trouver les valeurs de l'équation de la trajectoire ![]() à tous les temps
multiples d'un pas de temps suffisamment petit
à tous les temps
multiples d'un pas de temps suffisamment petit ![]() .
.
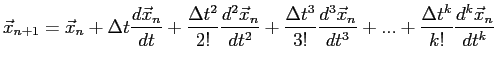 |
(2.2) |
où nous pouvons déduire la position à un temps n+1 en connaissant la position à un temps n.
Les deux position ![]() et
et
![]() sont séparées dans le temps de
sont séparées dans le temps de ![]() .
La plupart des méthodes utilisant cette voie pour résoudre les équations différentielles nécessitent
un judicieux mélange entre précision escomptée, temps de calcul et espace mémoire disponible.
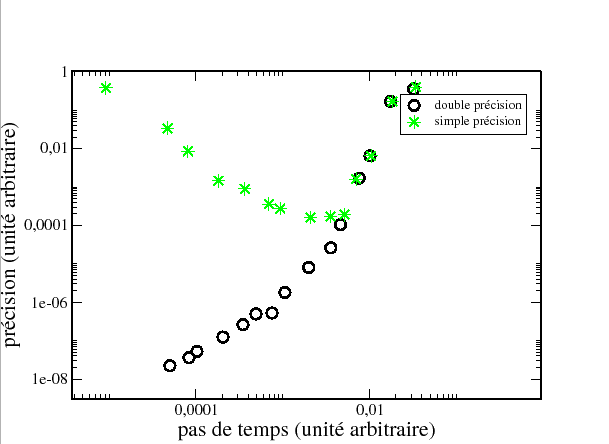
La précision du calcul n'est pas uniquement due à la petite valeur du pas de temps mais aussi
à la précision de la machine. En effet il ne faut pas oublier que l'ordinateur utilise des nombres
qui sont quantifiés et donc si nous prenons un pas de temps trop petit, l'erreur de quantification devient
telle que le calcul de la nouvelle position obtenue dans l'espace des phases n'est pas du tout correcte
car le nombre de pas et donc la somme des erreurs augmentent (Fig 2.1).
.
La plupart des méthodes utilisant cette voie pour résoudre les équations différentielles nécessitent
un judicieux mélange entre précision escomptée, temps de calcul et espace mémoire disponible.
La précision du calcul n'est pas uniquement due à la petite valeur du pas de temps mais aussi
à la précision de la machine. En effet il ne faut pas oublier que l'ordinateur utilise des nombres
qui sont quantifiés et donc si nous prenons un pas de temps trop petit, l'erreur de quantification devient
telle que le calcul de la nouvelle position obtenue dans l'espace des phases n'est pas du tout correcte
car le nombre de pas et donc la somme des erreurs augmentent (Fig 2.1).
|