suivant: Conditions de croissance monter: Comparaison avec les résultats précédent: Vérification de la géométrie Table des matières
La section efficace de production d'un composé lors d'une réaction est une mesure de sa probabilité d'apparition. La probabilité de former un composé lors d'une réaction chimique entre deux molécules A et B dépend de l'énergie d'impact entre A et B, et bien sûr du potentiel d'interaction entre A et B. Ainsi, pour une énergie d'impact donnée, nous pouvons simuler un grand nombre de réactions entre A et B, et donc comparer les proportions des différents produits formés avec les résultats d'expériences. Cette comparaison permet une des meilleures vérifications possibles car le potentiel ressenti par les atomes joue un rôle majeur dans la valeur des sections efficaces.
Dans un premier temps il est possible de vérifier que l'interaction Si-H est bien représentée.
Pour comparer les résultats de sections efficaces de création des produits
obtenus expérimentalement lors de la réaction ![]() [59,60] avec la simulation, il faut simuler un grand nombre
de trajectoires de collisions entre
[59,60] avec la simulation, il faut simuler un grand nombre
de trajectoires de collisions entre ![]() et
et ![]() pour des énergies d'impacts différentes.
Il faut ensuite calculer les probabilités d'apparition
des différents produits possibles pour toutes ces énergies d'impact.
Pour cela nous avons tiré de façon aléatoire des trajectoires suivant un paramètre d'impact
circulaire de rayon
pour des énergies d'impacts différentes.
Il faut ensuite calculer les probabilités d'apparition
des différents produits possibles pour toutes ces énergies d'impact.
Pour cela nous avons tiré de façon aléatoire des trajectoires suivant un paramètre d'impact
circulaire de rayon ![]() choisit entre 0 et
choisit entre 0 et ![]() .
Nous pouvons ainsi trouver les valeurs des sections efficaces simulées en
fonction de l'énergie d'impact avec
.
Nous pouvons ainsi trouver les valeurs des sections efficaces simulées en
fonction de l'énergie d'impact avec
![]() où P est la
probabilité d'avoir le produit considéré.
Par exemple, pour trouver la section efficace de production de
où P est la
probabilité d'avoir le produit considéré.
Par exemple, pour trouver la section efficace de production de ![]() nous utilisons
nous utilisons
![]() , où
, où
![]() représente le rapport entre le nombre de trajectoire qui ont
formé un produit
représente le rapport entre le nombre de trajectoire qui ont
formé un produit ![]() et le nombre total de trajectoires.
et le nombre total de trajectoires.
Lors de ces simulations, nous avons obtenus 5 % des trajectoires avec une
divergence énergétique supérieur à 1 % sur 20 ps.
Ainsi, nous avons éliminé les trajectoires qui ne conservaient pas
suffisamment l'énergie totale.
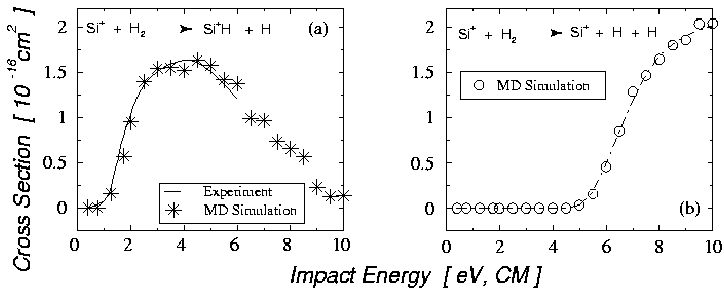
De cette façon, il nous a été possible de calculer la section efficace pour les produits issus
de simulations de la réaction
![]() (Fig 4.5) [61].
Les courbes de section efficace de production ainsi obtenues montrent
un très bon accord avec les valeurs expérimentales.
Ces simulations de réactions chimiques nous permettent donc de confirmer
la validité des potentiels de liaisons pour H-H et Si-H dans nos simulations.
En effet, si les potentiels étaient incorrects, les probabilités de
former des molécules lors de réactions chimiques avec une énergie d'impact
donnée seraient différentes.
De la même façon, nous avons vérifié l'accord entre les valeurs des sections
efficaces simulées et expérimentales dans le cas de réactions entre
(Fig 4.5) [61].
Les courbes de section efficace de production ainsi obtenues montrent
un très bon accord avec les valeurs expérimentales.
Ces simulations de réactions chimiques nous permettent donc de confirmer
la validité des potentiels de liaisons pour H-H et Si-H dans nos simulations.
En effet, si les potentiels étaient incorrects, les probabilités de
former des molécules lors de réactions chimiques avec une énergie d'impact
donnée seraient différentes.
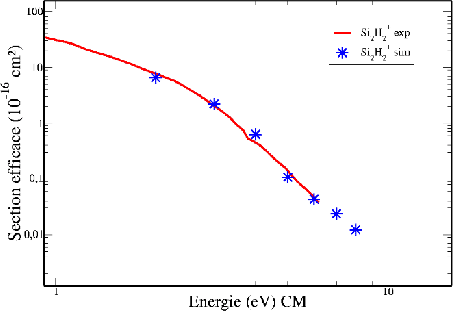
De la même façon, nous avons vérifié l'accord entre les valeurs des sections
efficaces simulées et expérimentales dans le cas de réactions entre ![]() et
et ![]() .
Cette simulation permet de vérifier notre potentiel entre les atomes de silicium
pour toutes les distances (Fig 4.6).
Pour réaliser cette étude qui peut être naturellement parallélisée, nous avons
développé une grappe de calculs sur les ordinateurs des salles de travaux pratiques
de l'Ecole Polytechnique.
.
Cette simulation permet de vérifier notre potentiel entre les atomes de silicium
pour toutes les distances (Fig 4.6).
Pour réaliser cette étude qui peut être naturellement parallélisée, nous avons
développé une grappe de calculs sur les ordinateurs des salles de travaux pratiques
de l'Ecole Polytechnique.
Un montage NFS (Network File System) permet d'avoir un espace disque commun à
toutes les machines.
De plus, une récupération des clefs privées de chaque machine du parc
informatique, permet d'effectuer une connexion cryptée en ssh sans l'utilisation
de mots de passe (voir l'annexe).
Nous pouvons donc faire un automate qui lance localement un script bash sur chaque machine,
tout en sauvegardant les résultats issus de chaque ordinateur dans un répertoire propre
à l'ordinateur qui a lancé la simulation.
Il devient donc possible d'écrire une série de scripts qui lancent, lors d'une connexion,
une simulation mettant en jeu les ressources de mémoires et de CPU de l'ordinateur appelé
à faire la simulation.
Ainsi, il est possible de créer un répertoire pour chacun des 130 ordinateurs disponibles,
et de lancer une simulation avec un paramètre d'impact ![]() différent sur chacun des ordinateurs de la grappe.
Une série de scripts a donc été écrite pour lancer des simulations sur un nombre
donné de machines, pour les stopper, et pour vérifier l'avancement des simulations.
Un grand nombre de trajectoires ( près de 10000 ) ont donc été calculées.
Les statistiques résultantes sont très bonnes et permettent de se rendre compte
de la validité de notre code.
différent sur chacun des ordinateurs de la grappe.
Une série de scripts a donc été écrite pour lancer des simulations sur un nombre
donné de machines, pour les stopper, et pour vérifier l'avancement des simulations.
Un grand nombre de trajectoires ( près de 10000 ) ont donc été calculées.
Les statistiques résultantes sont très bonnes et permettent de se rendre compte
de la validité de notre code.
|
|
Nous pouvons de cette façon, être certains que les différences obtenues avec l'expérience ne sont pas dues à des erreurs induites par une faiblesse dans le statistique. Ainsi, nous avons remarqué que l'accord, qui est très bon pour certaines espèces, peut se révéler médiocre si la paramétrisation n'est pas bien faite. C'est notamment le cas pour le carbone. En effet, les simulations de réactions chimiques avec le carbone pour le calcul des sections efficaces de production ont montré que des produits sont formés pour des faibles energies d'impact, alors que les expériences prouvent le contraire. Ceci se traduit par une valeur du potentiel modélisé du carbone qui est trop forte à grande distance. Nous voyons donc la nécessité de reparamétrer les valeurs semi-empiriques pour le calcul du potentiel du carbone [62]. Cependant dans le cas des interactions entre le silicium et l'hydrogène, l'accord est parfaitement acceptable. Nous pouvons en conclure que notre surface de potentiel représente une approximation suffisante.