suivant: Chaîne linéaire hétéroatomique monter: Description du modèle électronique précédent: Description du modèle électronique Table des matières
Dans cette approximation, chaque atome "![]() " de la chaîne possède un
hamiltonien
" de la chaîne possède un
hamiltonien
![]() dont nous supposerons connaître les états
propres
dont nous supposerons connaître les états
propres ![]() représentés par les fonctions d'ondes
représentés par les fonctions d'ondes
![]() soit:
soit:
| (3.1) |
Par simplicité, nous considérerons par la suite des atomes à un ou deux
électrons, n'ayant qu'une seule orbitale atomique
![]() . Pour fixer les idées,
. Pour fixer les idées, ![]() peut être l'orbitale hydrogénoïde 1s :
peut être l'orbitale hydrogénoïde 1s :
![]() où r est la distance au centre de
masse de l'atome
où r est la distance au centre de
masse de l'atome ![]() . Le point important est que cette fonction d'onde
décroît exponentiellement lorsque nous nous éloignons du centre, et reste donc
fortement localisée. Nous considérons donc qu'un électron ressent
essentiellement le potentiel atomique, ce qui nous suggère d'écrire
l'hamiltonien sous la forme:
. Le point important est que cette fonction d'onde
décroît exponentiellement lorsque nous nous éloignons du centre, et reste donc
fortement localisée. Nous considérons donc qu'un électron ressent
essentiellement le potentiel atomique, ce qui nous suggère d'écrire
l'hamiltonien sous la forme:
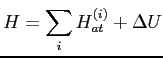 |
(3.2) |
Nous supposons que l'ensemble des fonctions d'ondes atomiques constitue une base de l'espace des états, si bien que la fonction d'onde d'un électron dans le cristal peut être décomposée sur cette base; nous pouvons donc prendre comme fonction d'onde des électrons une combinaison linéaire des orbitales atomiques, soit:
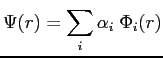 |
(3.3) |
où la somme se fait sur tous les atomes de la chaîne et où les ![]() sont des nombres complexes.
Si nous reportons la décomposition dans l'équation aux valeurs propres:
sont des nombres complexes.
Si nous reportons la décomposition dans l'équation aux valeurs propres:
![]() avec H donné par
avec H donné par
![]() , nous obtenons:
, nous obtenons:
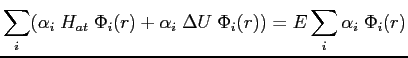 |
(3.4) |
En multipliant par ![]() et en intégrant sur tout l'espace, nous
obtenons:
et en intégrant sur tout l'espace, nous
obtenons:
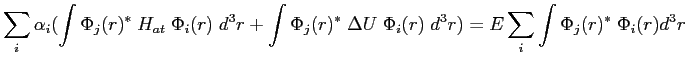 |
(3.5) |
Nous allons faire maintenant un certain nombre d'approximations reposant
sur le fait que les fonctions d'ondes atomiques ![]() sont
fortement localisées sur les sites.
sont
fortement localisées sur les sites.
1)
![]()
![]() est le symbole de Krönecker
(
est le symbole de Krönecker
(
![]() si
si ![]() et
et
![]() si
si ![]() ).
).
2) De même
![]()
où ![]() est l'énergie propre atomique.
est l'énergie propre atomique.
3) Les intégrales de transfert
![]() décrivent les sauts d'un électron d'un site i vers un site n.
décrivent les sauts d'un électron d'un site i vers un site n.
Nous supposons que l'électron
(i) ne peut sauter que sur un atome voisin du site i, les autres
intégrales de transfert étant négligeables.
(ii) cette intégrale ne dépend pas des atomes voisins, donc par symétrie nous
trouvons:
![]() que nous appelerons intégrale de saut. Soit au
total, en redéfinissant l'origine de l'énergie
que nous appelerons intégrale de saut. Soit au
total, en redéfinissant l'origine de l'énergie
![]() (qui n'a pas une valeur absolue mais relative) pour éliminer le terme
(qui n'a pas une valeur absolue mais relative) pour éliminer le terme
![]() : nous obtenons l'équation :
: nous obtenons l'équation :
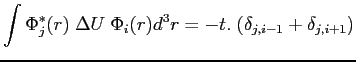 |
(3.6) |
Nous obtenons ainsi la composante de l'équation de Schrödinger associée à chaque site j d'un électron dans la chaîne:
Ce qui nous donne, en faisant varier j de 1 à N où N est le nombre
de sites occupés qui composent la chaîne, autant d'équations qu'il y a
d'atomes dans la chaîne. Nous obtenons donc N équations à N inconnues qui
sont les composantes ![]() sur chaque site. Ainsi, par diagonalisation
de la matrice formée par toutes ces équations, nous avons les niveaux
d'énergie possible de la chaîne. Nous obtenons ainsi l'énergie
électronique totale de la chaîne en sommant sur les niveaux occupés par
deux électrons (dégénerescence de spin).
sur chaque site. Ainsi, par diagonalisation
de la matrice formée par toutes ces équations, nous avons les niveaux
d'énergie possible de la chaîne. Nous obtenons ainsi l'énergie
électronique totale de la chaîne en sommant sur les niveaux occupés par
deux électrons (dégénerescence de spin).