suivant: Processus d'adsorption monter: Bilan énergétique des réactions précédent: Bilan énergétique des réactions Table des matières
Du point de vue de la physique statistique, nous pouvons considérer,
sur une trajectoire, notre système (agrégat + atome d'hydrogène)
comme un ensemble micro-canonique. Dans un ensemble micro-canonique,
nous avons une conservation du volume de l'espace des phases ![]() correspondant à l'énergie totale
correspondant à l'énergie totale ![]() de notre système décrit par un hamiltonien
de notre système décrit par un hamiltonien ![]() qui dépend des positions
qui dépend des positions ![]() et des impulsions
et des impulsions ![]() .
.
Nous pouvons ainsi obtenir l'entropie avec la relation de Boltzmann qui est la base de la physique statistique:
| (5.2) |
et donc la température avec la relation qui sert de définition pour l'entropie pour la thermodynamique.
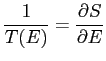 |
(5.3) |
Une façon générale de trouver la température est donc d'estimer le volume de l'espace
des phases qui entoure l'ensemble des trajectoires, puis de découper ce volume
en cellules élémentaires ![]() . Nous pouvons ensuite déduire la variation de ce nombre
de cellules élémentaires correspondant à une variation de
. Nous pouvons ensuite déduire la variation de ce nombre
de cellules élémentaires correspondant à une variation de ![]() à
à
![]() dans
ce volume.
Ainsi, il est possible d'estimer l'équation 5.1
et de suivre le développement ci-dessus qui permet d'obtenir la température.
dans
ce volume.
Ainsi, il est possible d'estimer l'équation 5.1
et de suivre le développement ci-dessus qui permet d'obtenir la température.
Cependant, les interactions inter-nucléaires étant classiques, des simplifications dans l'écriture de la fonction de partition sont possibles et permettent de trouver la température en utilisant la formule:
Où ![]() est la masse de l'agrégat,
est la masse de l'agrégat, ![]() est l'impulsion quadratique moyenne des atomes
de l'agrégat,
est l'impulsion quadratique moyenne des atomes
de l'agrégat, ![]() est le nombre de degrés de liberté,
est le nombre de degrés de liberté, ![]() la constante de Boltzmann
et T la température.
Pour une molécule non linéaire, le nombre de degrés de liberté de l'agrégat est
la constante de Boltzmann
et T la température.
Pour une molécule non linéaire, le nombre de degrés de liberté de l'agrégat est ![]() avec
avec
![]() le nombre d'atomes composant la structure.
En effet, soit
le nombre d'atomes composant la structure.
En effet, soit ![]() la fonction de partition qui normalise la statistique
des particules concernées:
la fonction de partition qui normalise la statistique
des particules concernées:
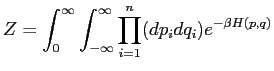 |
(5.5) |
Ou H est supposé fonction de ![]() et de
et de ![]() mais sans dépendance croisée entre la
position
mais sans dépendance croisée entre la
position ![]() et la l'impulsion
et la l'impulsion ![]() de la particule '
de la particule '![]() '
car
'
car
![]() contient le potentiel classique
contient le potentiel classique ![]() qui ne dépend que
de la position.
Nous posons la valeur canonique moyenne
qui ne dépend que
de la position.
Nous posons la valeur canonique moyenne
![]() comme la valeur
quadratique moyenne de l'énergie liée à la coordonnée normale
comme la valeur
quadratique moyenne de l'énergie liée à la coordonnée normale ![]()
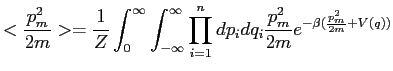 |
(5.6) |
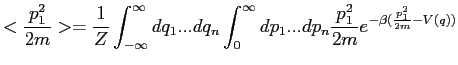 |
(5.7) |
En posant ![]() et
et
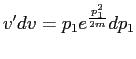 nous pouvons faire une
intégration par parties et obtenir:
nous pouvons faire une
intégration par parties et obtenir:
![$\displaystyle \int_0^\infty p_1^2e^{\frac{p_1^2}{2m}}dp_1 = [-p_1 \frac{m}{\bet...
...}]_0^{\infty} -\int_0^{\infty} -\frac{m}{\beta} e^{-\beta \frac{p_1^2}{2m}}dp_1$](img384.png) |
(5.9) |
La premier terme de l'intégration par parties étant nul, et sachant que
![]() nous obtenons:
nous obtenons:
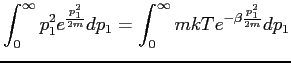 |
(5.10) |
Nous pouvons ensuite réinjecter cette équation dans 5.8 pour obtenir
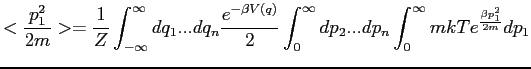 |
(5.11) |
Nous remarquons ensuite en replaçant ![]() dans les variables d'intégration sur l'ensemble de
dans les variables d'intégration sur l'ensemble de ![]() que la fonction
que la fonction ![]() réapparaît.
Ainsi, nous obtenons l'équation cherchée:
réapparaît.
Ainsi, nous obtenons l'équation cherchée:
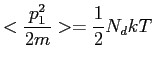 |
(5.12) |
dans laquelle ![]() est une des coordonnées généralisées ce qui est l'équivalent à un
degré de liberté. L'application de ce développent nous est apparut important pour
comprendre ce que pouvait être la température pour de petit système comme les agrégats
que nous étudions. En effet, même s'il est facile de comprendre ce qu'est une température
pour un gaz parfait, il n'en est pas du tout de même pour les agrégats en suspension
dans ce gaz.
Ainsi, en utilisant la formule 5.4, nous pouvons obtenir la variation de la température
pour chacun des processus.
Nous constatons que, lors d'une mesure de la variation de température après des impacts avec
de l'hydrogène atomique, l'agrégat est chauffé quelque soit le procédé, sauf
bien sûr dans le cas d'une collision élastique où l'agrégat ne subit pas de variation de
température.
La hausse de température lors d'une réaction avec de l'hydrogène
atomique est inversement proportionnelle à la taille de l'agrégat.
La variation
de température pour des agrégats de six atomes silicium, atteint 1500 K alors que
dans le cas d'une réaction sur un agrégat de vingt atomes de silicium, la variation
de température n'est plus que de 200 K.
Nous pouvons voir sur la figure 5.8 que, dans le cas d'un agrégat de
est une des coordonnées généralisées ce qui est l'équivalent à un
degré de liberté. L'application de ce développent nous est apparut important pour
comprendre ce que pouvait être la température pour de petit système comme les agrégats
que nous étudions. En effet, même s'il est facile de comprendre ce qu'est une température
pour un gaz parfait, il n'en est pas du tout de même pour les agrégats en suspension
dans ce gaz.
Ainsi, en utilisant la formule 5.4, nous pouvons obtenir la variation de la température
pour chacun des processus.
Nous constatons que, lors d'une mesure de la variation de température après des impacts avec
de l'hydrogène atomique, l'agrégat est chauffé quelque soit le procédé, sauf
bien sûr dans le cas d'une collision élastique où l'agrégat ne subit pas de variation de
température.
La hausse de température lors d'une réaction avec de l'hydrogène
atomique est inversement proportionnelle à la taille de l'agrégat.
La variation
de température pour des agrégats de six atomes silicium, atteint 1500 K alors que
dans le cas d'une réaction sur un agrégat de vingt atomes de silicium, la variation
de température n'est plus que de 200 K.
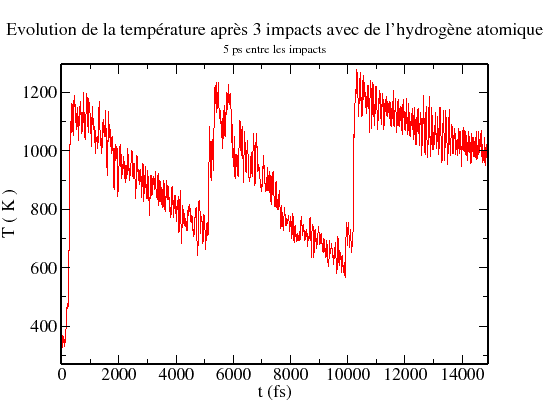
Nous pouvons voir sur la figure 5.8 que, dans le cas d'un agrégat de
![]() ,
les réactions (ici 3) avec de l'hydrogène atomique chauffe très rapidement l'agrégat.
Nous pouvons aussi noter que l'élévation de température est relativement constante ( 700 K ).
Dans cette simulation de trois réactions, nous avions obtenu une absorption d'hydrogène
suivie d'une recombinaison puis une autre absorption.
Des simulations indépendantes confirment nos résultats quant à
la stabilité des agrégats de silicium pour des températures aussi élevées [94].
,
les réactions (ici 3) avec de l'hydrogène atomique chauffe très rapidement l'agrégat.
Nous pouvons aussi noter que l'élévation de température est relativement constante ( 700 K ).
Dans cette simulation de trois réactions, nous avions obtenu une absorption d'hydrogène
suivie d'une recombinaison puis une autre absorption.
Des simulations indépendantes confirment nos résultats quant à
la stabilité des agrégats de silicium pour des températures aussi élevées [94].
|
Le calcul de la variation de température subie lors des impacts permet de voir une élévation de température lors d'une réaction avec l'atome d'hydrogène, qu'il soit capté ou recombiné. Ceci est étonnant au premier abord en faisant le bilan d'énergie.
| Enthalpie de formation | 3.89 |
2.77 |
4.5 eV | 3.20 |